Introduction To AI

Hello and welcome to this introductory series on Artificial Intelligence!
AI is a branch of computer science that engages in developing intelligence for machines - learning, perception of objects, reasoning, processing of natural languages (understanding a real language like English). Over recent decades with the growth in computing power, AI research has accelerated greatly and nowadays computers are already accomplishing a lot - cars that drive by themselves, computers that beat the best Jeopardy champions and even the best DotA players. In the next few posts we'll learn about concepts of AI and machine learning in particular alongside code examples and demos written in JavaScript. 
The first topic in the series is Graph Theory, a basic subject in computer science, but before we begin with all the formality let us travel back in time and witness how a theory is born.

​The Seven Bridges Problem

Back in the 1700s, the city Königsberg, Prussia was built on the Pregel River, which divided the city into four districts connected by seven bridges. Every week, the people of the city contemplated on a question while taking their Sunday stroll - can a person find a path that passes through all districts while crossing every bridge only once?

Map of Königsberg, Prussia in 1652 (by Meiran-Erben).

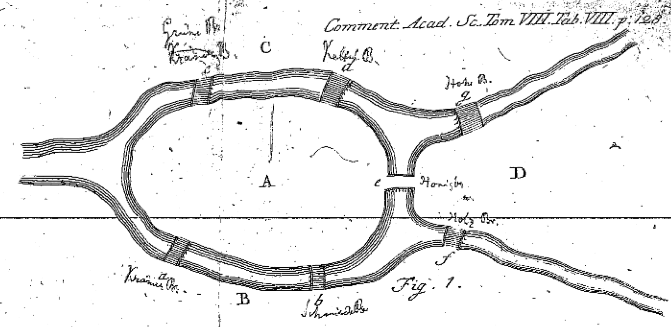
The problem turned to be so difficult they had to ask famous mathematician Leonard Euler for help. At first Euler didn't really want to bother with such a trivial problem, but he gave in eventually and proved that no such path exists. Geometry or Algebra were not sufficient to solve the problem and Euler had to get creative - he noticed that only the districts and bridges are important to the problem, and he can get rid of all other information (like the structure inside each district). He also saw that any time one enters a district through a bridge, he has to leave through another. He inferred that if a district is passed through only once it has to be at the beginning or the end of the path. This means that only the beginning and end points are visited an odd number of times in contrast to other districts. Since all bridges must be crossed and district A has 5 bridges connected to it and districts B, C and D have 3, Euler deduced that there is no such path.
In 1735 Euler published a paper with the solution alongside a generalization of the problem for any number of districts and bridges, little did he know that this paper will become the basis of a whole new branch of mathematics.

Euler's abstraction of Königsberg districts and bridges.

​Graph Theory

A Graph is a collection of nodes (or vertex) and edges which correlate to a relation of some sort between a pair of nodes.
Graphs and graph theory techniques are used in many fields to solve practical problems: In sociology graphs are used to track friendships between people and to create social networks, we can also use graphs for creating a map of cities and the roads that connect them.
Graphs are used a lot in computer science, for example, to find an optimal route between two computers in a network. Finite-state machines are also naturally represented by graphs. 
Basically, graphs help us represent any set of objects that are related to each other in an elegant manner. 

Fig 1. An undirected graph that connects the biggest cities of Israel.

Edges of a graph can be either directed or undirected, directed edges have orientation - an edge from node A to node B is not the same as an edge from B to A while undirected edges are the opposite, for instance in Figure 1 we take the same road from Tel Aviv to Jerusalem and vice versa.
Edges may also have weights - numbers that are given to them and depict a cost, e.g. the length of the roads in Figure 1.
To sum up - a graph $G$ is made of nodes $V(G) = \{ n_1, n_2, ... \,, n_k\}$, edges $E(G) = \{ (n_i, n_j)\}$ where $(n_i, n_j)$ represents an edge from $n_i$ to $n_j$. If the graph is weighted - a weight function $W(n_i, n_j)$. 

Fig 2. A state machine depicted by a directed graph.

​Pathfinding

One of the most obvious problems that arise in graph-theory is pathfinding - finding the optimal route from one node to another.
Pathfinding has a primary role in robotics and video-games, it gives robots and characters the ability to move and avoid obstacles, and most notably, pathfinding algorithms are used by GPS navigation systems to help us reach our travel destinations. 
Pathfinding divides into two problems:

1. Finding a route between two given nodes.
2. Finding the optimal shortest route between two given nodes.

More formally, given a graph and two nodes $(G, s, t)$, find a (minimal) set of edges that begins with $s$ and ends with $t$.
The general method to solve these problems is to start from a node and explore some of its adjacent nodes. Rudimentary algorithms will check every single neighbor until finding the destination but smarter ones will extract data from the graph and use it to explore only viable options.
Let's see algorithms that solve each of these problems.

​Breadth-first search

BFS is a basic algorithm that solves the second problem - it finds a path between two given nodes that is guaranteed to be optimal (on graphs with no weight functions).
It does so by searching the immediate neighbors of $s$ before moving to higher-level neighbors.
Think of the "search zone" as a circle with an expanding radius, first all nodes that are 1 node away are scanned, then all nodes that are 2 nodes away and so on.  To achieve this effect, we use a queue to explore - vertices that go in first get visited first.
A cool thing about BFS is that it finds the shortest path from $s$ to all other nodes in the graph (if we don't stop it when finding the destination node).

​Depth-First Search

Unlike breadth-first search, DFS finds a path that is not guaranteed to be optimal between two nodes. The idea behind it is to always explore one adjacent node to the current one, unlike BFS that searches all of the neighbors first. 
Intuitively, we can think of it as always moving forward until getting stuck, like you would do in a maze. This is done using a stack instead of a queue.

As you can see in example 2, DFS did not find the shortest path, but it did find a path faster than BFS.
One can infer that using BFS is preferable when the graph is dense and short taking advantage of the "radius searching" method while DFS is better used on a sparse and tall graph with the "moving forward" method.

​Dijkstra's Algorithm

Dijkstra's algorithm finds the shortest path between two nodes in a directed and weighted graph using the relaxation technique. It is a greedy algorithm that chooses to explore the node that is closest to the root and updates the distances to all nodes connected to it (relaxing outgoing edges). Simply put - the algorithm chooses to explore the closest nodes to the source first and the greedy choice guarantees that if a node is being explored, its route will be the shortest.

You may have noticed that Dijkstra's algorithm is a generalization of BFS that respects weights (BFS is Dijkstra's algorithm where all weights equal 1), and like BFS, this algorithm finds the shortest path from the source to all other nodes in the graph.
Another thing to note is that this method does not work if the graph has a negative weight (the greedy choice of the next explored node won't work).

​A-star Search

A* is an improvement upon Dijkstra's algorithm that uses heuristics, which is just fancy word for educated guesses.
As opposed to Dijkstra's method that only takes the distance from the source to other nodes into consideration when exploring, A* adds the distance from the nodes to the destination. How do we know this distance? we don't, and that's what the heuristic function is for - we estimate it. The nice thing is that we only need to calculate the heuristic once, and use it as many times as we want since the distances won't change in most practical applications (we pre-process the heuristic function). This means that A* will only explore nodes that seem closer to the goal node and move in its general direction.

In example 4 we see a huge improvement on the same graph as in example 3 with a heuristic function - the euclidean distance (aerial distance) from each node to the goal. A* makes sure to explore attractive nodes first (nodes that seem closer to the goal) and advances through the graph much quicker.
A* variations are widely used as a pathfinding algorithm - from GPS systems to video game characters movement 

Note
In order for A* to work properly, the heuristic function needs to be monotonic - for each node $n$ and neighbor $n'$, $h(n) \le w(n, n') + h(n')$. In most practical problems this turns to be the case.

Pathfinding in real life

A* variations are widely used in most practical applications where pathfinding is needed. In the demo below, we'll see how robot vacuum cleaners choose their path and move between obstacles, the furniture in a room, using A*.

​Conclusion

In this first post of the series we learned how Graph Theory was conceived by a rather trivial question, we learned what graphs consist of and explored different algorithms for traversing graphs in the optimal way. Finally - we saw a live demo of a practical problem solved with the A* algorithm - navigation of robots in a room full of obstacles.
In the next post we'll learn about Clustering which is a way of classifying data sets to groups with similar traits, stay tuned!

Further Reading

1. ​IBM's Watson supercomputer beats Jeopardy champions (Youtube).
2. OpenAI beats Dendi at 1 vs. 1 SF in Dota 2 (Youtube).
3. Leonard Euler's Solution to the Königsberg Bridge Problem.
   
4. An Interview With Edsger W. Dijkstra.